Open and Closed Refinement Semantics for Models

Book section 13.7.1 Open and closed refinement semantics (page 265, revised here)

If you show someone a diagram of a house, like the one at the left of Figure 13.7, that has no garage, should they assume the house has no garage? Or is it OK for you to later provide a more detailed diagram that includes a garage? That is, can they rely upon the absence of something in their reasoning? You as the author of the diagram know the answer and you should let readers know what rules you are using for refinement. You can communicate your intentions by committing to either open or closed refinement semantics.

• Open semantics. In refinement with open semantics, the refinement can introduce whatever new items it pleases. In the example, adding a new garage or storey in the refinement is OK, as would be chicken coops and windmills.

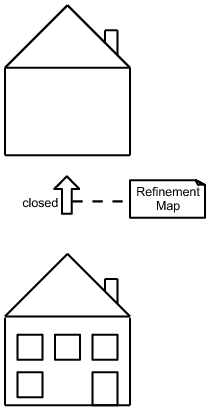
• Closed semantics. In refinement with closed semantics, you restrict what kinds of new details can be introduced in the refinement. It’s best to list the categories of what may be introduced via refinement in the refinement map.

In the house example, using closed semantics, you might categorically restrict the refinement so that no new garages or storeys are introduced. Things you do not mention in the list are OK to introduce, such as new windows or chimneys, so you still have an opportunity to add details. A common choice is to prohibit the addition of the kinds of items already shown in the low-detail model. For example, since the left side of Figure 13.7 shows a chimney, closed refinement semantics would prohibit the refinement from adding more chimneys, but since windows are not shown, any number of windows could be added. Figure 13.8 shows the house example with both open and closed semantics refinement.

Open semantics is clearly easier for you as an author because it does not force you to commit or even think about restrictions on the refinement. But closed semantics is clearly easier for readers since it gives them more firm ground to stand on and draw conclusions. In documentation with lots of readers, use closed semantics if you can. Either way, always let readers know which semantics you are using.

Figure 13.7: Refinement is a relationship between a high- and low-detail representation of the same thing. In this diagram, refinement is used to relate a high-detail representation of a house (the right one, with three dimensions) with a low-detail representation (the left one, with two dimensions). The higher-detail representation is not always the more useful one. A refinement map is rarely written down, but it relates the elements from one representation to the other.

Figure 13.8: The kind of refinement semantics determines what details can be introduced. In this example, the closed semantics categorically restricts the refinement so that no new garages, chimneys, or storeys are introduced. With open semantics, there are no such restrictions. In software architecture, it is best to follow closed semantics and prohibit new ports from being added.

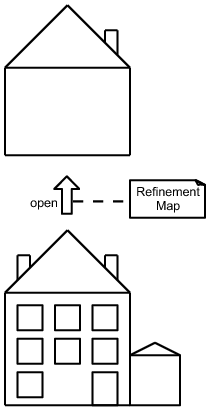(a) Closed semantics: Categorical exclusion of added elements. In this case, the categories allowed are windows; all else is disallowed.	(b) Open semantics. Anything can be added, including the windows, chimneys, and garage.

This section is extracted from the book.